Blogsheet week 10
In this week’s lab, you will collect more data on low pass
and high pass filters and “process” them using MATLAB.
PART A: MATLAB
practice.
1. Open MATLAB. Open the editor and copy paste
the following code. Name your code as FirstCode.m
Save
the resulting plot as a JPEG image and put it here.
clear all;
x = [1 2 3 4 5];
y = 2.^x;
plot(x, y, 'LineWidth', 6)
xlabel('Numbers', 'FontSize', 12)
ylabel('Results', 'FontSize', 12)
2. What does clear all do?
This clears all previous data held in
Matlab currently.
3. What does close all do?
Closes any windows currently open.
4. In the command line, type x and press enter. This is a matrix. How
many rows and columns are there in the matrix?
There are five rows and one column.
5. Why is there a semicolon at the end of the
line of x and y?
This signifies the end of the line of
code.
6. Remove the dot on the y = 2.^x; line and
execute the code again. What does the error message mean?
“Error using ^
Inputs must be a
scalar and a square matrix.
To compute
elementwise POWER, use POWER (.^) instead.”
7. How does the LineWidth affect the plot?
Explain.
It makes the width of the plot line
wider. For example, the original line
width was 6. The following image is the
same plot using a line width of 30.
8.
Type help
plot on the command line and study the options for plot command. Provide how you would change the line for plot command to obtain the following
figure (Hint: Like ‘LineWidth’, there
is another property called ‘MarkerSize’)
We would add “
'-or','MarkerSize', 12” to the code. Where “-or” signifies making the plot red and
the ‘MarkerSize, 12” code make the markers large.
9.
What happens if you change the line for
x to
x
= [1; 2; 3; 4; 5]; ? Explain.
Nothing changes. The graph stays the same both times.
10.
Provide the code for the
following figure. You need to figure out the function for y. Notice there are
grids on the plot.
11.
Degree vs. radian in MATLAB:
a.
Calculate sinus of 30 degrees using a calculator
or internet.
Sin(30) = 0.5
b.
Type sin(30) in the command line of the MATLAB. Why
is this number different? (Hint: MATLAB treats angles as radians).
The answer of radians is (-0.9880).
This is because it’s in radians.
c.
How can you modify sin(30) so we get the correct
number?
We can convert 30 degrees into radians by multiplying by pi an divide by
180.
12.
Plot y =
10 sin (100 t) using Matlab with two different resolutions on the same plot: 10 points per period and
1000 points per period. The plot needs to show only two periods. Commands you might need to use are linspace, plot,
hold on, legend, xlabel, and ylabel. Provide your code and resulting figure.
The output figure should look like the following:
clear all;
close all;
t = linspace(0,((4*pi)/100),10);
x = 10*sin(100*t);
f = linspace(0,((4*pi)/100),1000);
y = 10*sin(100*f);
plot(t,x, '-or');
hold on;
plot(f,y);
xlabel('Time (s)', 'FontSize', 12)
ylabel('y function', 'FontSize', 12)
13.
Explain what is changed in the following plot
comparing to the previous one.
The fine graph is clipped at a maximum
positive amplitude of 5.
14.
The command find
was used to create this code. Study the use of find (help find) and try to replicate the plot above. Provide your code.
clear all;
close all;
t = linspace(0,((4*pi)/100),10);
x = 10*sin(100*t);
f = linspace(0,((4*pi)/100),1000);
y = 10*sin(100*f);
y(find(y > 5)) = 5;
plot(t,x, '-or');
hold on;
plot(f,y);
xlabel('Time (s)', 'FontSize', 12)
ylabel('y function', 'FontSize', 12)
15.
Create a code that would
clip the negative part of the sinusoidal signal for the fine plot to -5.
clear all;
close all;
t = linspace(0,((4*pi)/100),10);
x = 10*sin(100*t);
f = linspace(0,((4*pi)/100),1000);
y = 10*sin(100*f);
y(find(y < -5)) = -5;
plot(t,x, '-or');
hold on;
plot(f,y);
xlabel('Time (s)', 'FontSize', 12)
ylabel('y function', 'FontSize', 12)
PART B: Filters and
MATLAB
1.
Build a low pass filter using a resistor and
capacitor in which the cut off frequency is 1 kHz. Observe the output signal using
the oscilloscope. Collect several data points particularly around the cut off
frequency. Provide your data in a table.
2.
Plot your data using MATLAB. Make sure to use
proper labels for the plot and make your plot line and fonts readable. Provide
your code and the plot.
x = [5 10 20 30 40 50 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 2000 3000 4000];
y = [4.72 4.23 3.14 2.4 1.9 1.56 .83 .420 .292 .222 .180 .156 .136 .126 .114 .103 .098 .091 .082 .077 .061 .048 .040];
plot(x, y,'g', 'LineWidth', 6)
xlabel('Frequency ', 'Fontsize', 12)
ylabel('V Peak ','FontSize', 12)
hold o
n;
3.
Calculate the cut off frequency using MATLAB. find command will be used. Provide your
code.
x = [5 10 20 30 40 50 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 2000 3000 4000];
y = [4.72 4.23 3.14 2.4 1.9 1.56 .83 .420 .292 .222 .180 .156 .136 .126 .114 .103 .098 .091 .082 .077 .061 .048 .040];
plot(x, y,'g', 'LineWidth', 6)
xlabel('Frequency ', 'Fontsize', 12)
ylabel('V Peak ','FontSize', 12)
hold on;
t=find(y==400);
x(t)
4.
Put a horizontal dashed
line on the previous plot that passes through the cutoff frequency.
5.
Repeat 1-3 by modifying the circuit to a high
pass filter.
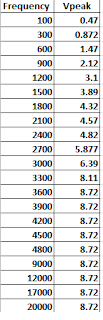
x = [100 300 600 900 1200 1500 1800 2100 2400 2700 3000 3300 3600 3900 4200 4500 4800 9000 12000 17000 20000];
y = [0.47 .872 1.47 2.12 3.1 3.89 4.32 4.57 4.82 5.877 6.39 8.11 8.72 8.72 8.72 8.72 8.72 8.72 8.72 8.72 8.72];
plot(x, y, 'LineWidth', 6)
xlabel('Frequency ', 'Fontsize', 12)
ylabel('V Peak ','FontSize', 12)
hold on;
6.
Repeat #4 for #5.